Как быстро считать ходы.

Нарды игра динамичная. Уровень мастерства определяется не только правильными ходами, но и, как нестранно, быстротой выполнения хода. В игре часто соперники соревнуются в скорости выполнения ходов настолько, что сторонний наблюдатель не успевает уследить ни за ходами, ни за зариками. Естественно, для того чтобы делать ходы с максимальной скоростью необходимо уметь быстро считать варианты ходов. Многие начинающие игроки после выброса зариков начинают пальцем считать ходы. Сначала первый вариант, потом второй… игра становится нудной, неинтересной, пропадает динамизм, острота, азарт. Вынести такую кару можно, если ставка в игре большая, и она может компенсировать с лихвой тягучесть игры.

Приведем несколько приемов, позволяющих научить быстро считать ходы:

- разметка доски;

- законы модулярной математики по модулю 6;

- научиться считать куши;

- счет до шести;

- счет после шести;

- двухцветная доска.

 

Разметка доски.

 

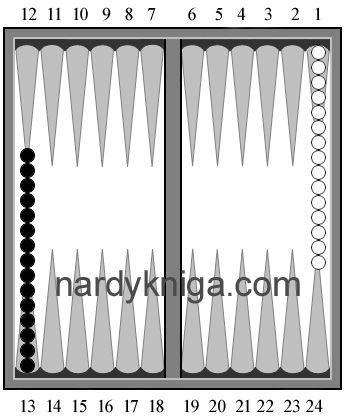
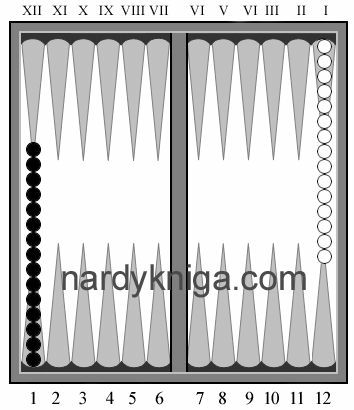На рис.1,2,3 представлены три варианта разметки доски. На рис.1 разметка от 1-го до 24-х. На рис.2 верхняя часть доски 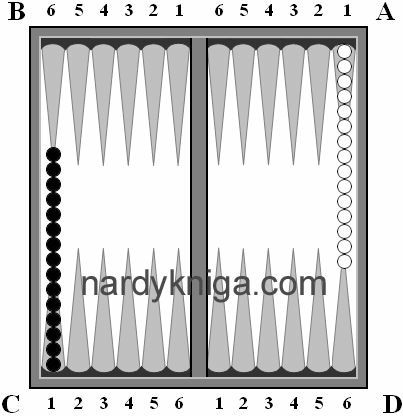пронумерована римскими цифрами от единицы до двенадцати. На нижней части нумерация  также  от  единицы до двенадцати, но использованы уже арабские цифры. На  рис.3  нумерация состоит  в  следующем:  каждая   четверть пронумерована от 1 до 6, а четверти обозначены латинскими буквами А, В, С, D. Если иметь перед глазами доску и запись ходов, например ход 5:5 для белых: рис.1 – 1:21; рис.2 – I:9; рис.3 – А1 – D3, то для записи ходов проблем с выбором нумерации доски нет. Нумерацией пользуются такой, которая привычна и удобна для игрока. Но если нумерацию доски необходимо использовать для облегчения подсчета ходов, то наиболее удобная для этих целей доска с нумерацией, представленная на рис.3.

Рекомендуем начинающим игрокам нанести такую нумерацию на доске, которую они используют для игры. И использовать ее во время игры для облегчения подсчета ходов.

Законы модулярной математики по модулю 6.

Людям неискушенным в математике, не следует бояться не только самого слова математика, но и такого «страшного» выражения, как модулярная математика. Не следует бояться его по той простой причине, что с необходимым минимумом знаний законов модулярной математики сталкивается абсолютно каждый человек ежедневно. И скорее всего не один раз в день.

Рассмотрим два примера. В первом примере выступает обычная математика, во втором примере модулярная математика по модулю 12.

Пример 1.  6 + 7 = 13;   2 + 3 = 5

Пример 2.  6 + 7 = 1;     2 + 3 = 5

На первый взгляд непонятно почему при сложении двойки с тройкой получается одно и то же число – 5, а вот при сложении шестерки с семеркой получаем разные числа – тринадцать и один. Чтобы понять почему так происходит надо посмотреть на левую руку (в большинстве случаев) и обнаружив там часы сразу становится ясно, что если к шести часам утра прибавить семь часов, получим один час пополудни. Вот и весь фокус с таким грозным названием как модулярная математика. В модулярной арифметике мы имеем дело с циклически замкнутыми конечными группами чисел, подобно числам на циферблате часов.

Но в примере с часами вычисления идет по модулю 12 (или mod 12), а в примере с нардами необходимо делать вычисления по модулю (mod 6).

Как делать вычисления по (mod x)? Вначале производим сложение, умножение по законам обычной арифметики, а затем, если мы хотим узнать ответ по (mod x), мы делим результат, полученный на предыдущем этапе, на х и записываем остаток. Этот остаток и является ответом на по (mod x). Чтобы найти ответ в примере с пятым кушом по модулю (mod 6), мы поступим следующим образом:

5 х 4 = 20

20 : 6 = 3, остаток 2

5 х 4 = 2 (mod 6)

Вычислим, к примеру, рядовой бросок 5:3 по (mod 6)

8 : 6 = 2 (mod 6)

Исходя из законов модулярной математики по (mod 6) бросок 5:3 и бросок 5:5 равен одному и тому же значению – 2.

Как это использовать рассмотрим далее.

Подсчет кушей.

Проще всего в выполнении ходов и их подсчет это кушевой бросок. С кушем 1:1 вопросов нет. Наглядно видно можно его выполнить или нет, так как длина хода равна четырем.

Куш 2:2 можно подсчитать несколькими 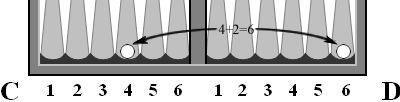способами.

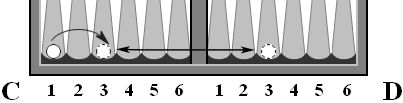
-делаем мысленно одно перемещение из четырех, например,  с С1 на С3 и затем смотрим на порядковый номер лунки (в нашем случае С3, с порядковым номером 3), и ставим камень на следующее поле в лунку с таким же порядковым номером (в нашем примере – D3), рис. 4.

- с применением модулярной арифметики два умножаем на четыре, получаем восемь. Восемь делим на шесть (можно поступить проще – от восьми отнять шестерку), получаем 2. Далее смотрим где стоит играющий  камень, (рис.5) например на С4. Порядковый номер  - четыре. К 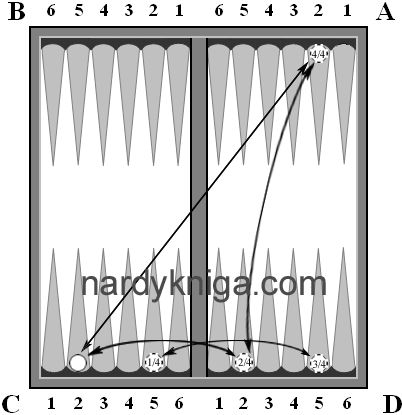четырем добавляем два, получаем шесть. Следовательно ход будет сделан на следующее, за полем С, поле D в лунку с порядковым номером шесть (D6).

Куш 3:3 надо разбить на четыре варианта – 1/4 хода; 2/4 хода;  3/4 хода 4/4  хода (рис.6).

Полный ход играется через два поля и камень ставится в лунку с тем же порядковым номером, с которого стартовал  камень. Особенность этого куша состоит в том, что порядковые номера при выполнении ходов совпадают не только на старте и финише, но и стартовый порядковый номер равен 2/4 ходу и равен, как отличалось ранее 4/4 ходу.

Так же порядковый номер 1/4 хода равен порядковому номеру лунки при выполнении 3/4 хода.

Касательно хода 3:3 в призме модульной арифметики имеем: 3 х 4 = 12 : 6 = 0 (mod 6).

Куш 4:4. разобьем этот ход на четыре части, как делали до этого с кушом 3:3. Допустим, изначально камень, которым надо ходить стоит на С3 (рис.7). полный ход (16 пунктов) можно 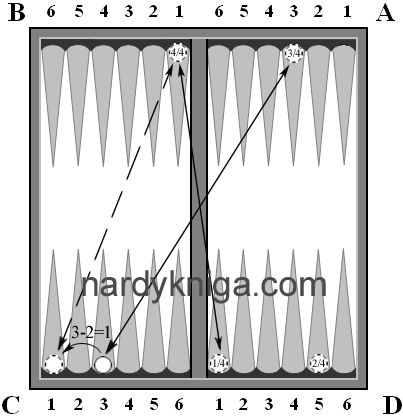подсчитать следующим образом – от лунки, где стоит стартующий камень отнимаем два очка и переместившись на три поля вперед получим финишный пункт. Смотрим на рис.7. С3 минус два равно С1, переносимся на три поля вперед, получаем лунку с порядковым номером 1 на поле В, то есть В1.

Особенность куша 4:4 состоит в том, что порядковые номера лунок совпадают в двух случаях: старт = 3/4 хода; 1/4  хода = 4/4 хода.

Разберем этот  куш с помощью полюбившийся нам модулярной арифметики. 4 х 4 = 16 : 6 = 4 (mod 6).

К стартовой лунке (номер 3) добавляем 4, получаем 7. Семь минус 6, равно 1. Все сходится С3 – В1.

Куш 5:5. Разбивать куш на четыре части, как делалось до этого с кушами 3:3 и 4:4, нет необходимости. Для быстрого подсчета хода 5:5 воспользуемся 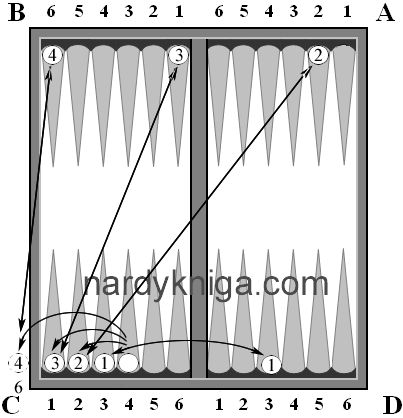следующей методикой. Обратимся к стартовому камню (рис. 8), он стоит на С4. Теперь мысленно, от стартующего камня удалимся влево на 1, 2, 3, 4 пункта. Для четвертого «удаления» придется мысленно «дорисовать» виртуальное поле, находящееся между полями В и С и напишем для него виртуальную лунку с порядковым номером 6. Вернемся к стартующему камню на С4 и первое удаление – С3. Так вот это первое удаление нам покажет порядковый номер лунки куда надо сделать первое перемещение – порядковый номер первого перемещения – тройка. Посмотрим на второе удаление от стартующего камня. Определим это удаление по цифре 2 внутри камня. Второе удаление указывает на С2, что автоматически обозначает, что второй ход от стартующего камня должен будет выполнен на лунку с порядковым номером – 2. В нашем примере это пункт А2. Третье удаление указывает на С1, что обозначает что третий ход должен выполнен на лунку с порядковым номером 1. В нашем примере это В1. И четвертое удаление от стартующего камня приводит к виртуальной лунке с шестым порядковым номером. Следовательно, четвертый, заключительный ход пятого куша должен быть сделан на лунку с порядковым номером – 6. В нашем примере это пункт В6.

Если стартующий камень стоит далее четвертой лунки или на второй и далее четверти, то для полного хода 5:5 потребуется более одного камня.

И закончим разбор хода 5:5 с применением модулярной математики

5 х 4 = 20 : 6 = 2 (mod 6)

C4 + 2 = 6 = В6.

Куш 6:6. Рассмотрев все куши до шестого, становится ясно, что с шестым кушом, как и с первым проблем не должно возникнуть в вопросе подсчета ходов. Простота в отношении хода 6:6 состоит в том, что стартующий камень ходит по всем четвертям на лунки с одним и тем же порядковым номером, равным порядковому номеру стартующего камня. Хотя, в отношении куша 6:6, уместней будет сказать не камня, а камней, так как для полного хода одного камня будет недостаточно (за исключением одного варианта).

Счет до шести.

Подсчет ходов до шести составляет небольшую трудности в отношении чисел 4 и 5, и тогда, когда приходится делать переход с одной четверти на другую. Когда ход выполняется на одной четверти, то с его выполнением трудностей не возникает. Приведем 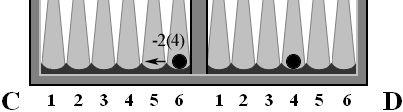пример, как быстро подсчитать ход четверкой пятеркой с одновременным переходом с одной четверти на другую.

На рис. 9 показан пример расчета хода пятерки. Берем стартующий камень, в нашем примере это камень на С4, отступаем от него один пункт влево, оказываемся на С3. Значит тройка – это лунка с порядковым номером, куда необходимо сделать ход. Второй вариант – отнятие одного пункта осуществляется уже после хода. С С4 ходим (мысленно) на D4, а затем от D4 отнимаем один пункт и оказываемся на D3. Вот, туда и надо сделать реальный ход.

На рис. 10 показан пример подсчета хода четверки. Делается аналогично, как и с ходом пятерки, но от стартующего камня необходимо отступать не один, а два пункта. С6 – 2 = 4 = D4.

Счет после шести.

Счет после шести можно разделить на два варианта. Первый вариант – счет после шести на двух четвертях. Второй вариант – счет после шести на трех четвертях.

Счет на двух четвертях проводится следующим образом – берется стартующий камень (напр. С1 на рис.11), запоминается его порядковый номер (в нашем примере – 1), далее разбиваем длину хода, которую нужно сделать из двух составляющих – первая составляющая – 6, вторая составляющая – разница в вычитании - длина хода минус 6. Например, на зариках выпало 5:3. В сумме – 8. Восемь – длина хода. Восемь минус шесть равно два. Эту разницу, равную двум, добавляем к порядковому номеру 1, получаем 3. Следовательно, полный ход должен выполнен с  С1 на следующее поле, поле D, на лунку, с порядковым номером 3, то есть на D3. Описать это можно следующей формулой.

Ход   7 = ПНСК + 1 следующая четверть от СК

Ход   8 = ПНСК + 2 следующая четверть от СК

Ход   9 = ПНСК + 3 следующая четверть от СК

Ход 10 = ПНСК + 4 следующая четверть от СК

Ход 11 = ПНСК + 5 следующая четверть от СК

Где ПНСК – порядковый номер стартующего камня, СК – стартующий камень.

Посмотрим на рис. 11, на поле D видим, как выполнить хода от 6 до 11, камнем, стоящим на С1. Обратимся теперь к самому сложному вопросу в подсчете ходов – счет после шести на трех четвертях. Подсчет таких ходов можно описать следующей формулой.

ДХ + ПНСК – 12 = ПН, где

ДХ – длина хода;

ПНСК – порядковый номер стартующего камня;

12 – расчетный коэффициент;

ПН – порядковый номер.

Посмотрим на рис. 12. Стартующий камень стоит на С4. Выбросив любой ход до 8, игрок рассчитывает ход по методикам рассмотренным ранее. Ход с длиной более 8, необходимо сделать вторую четверть от стартующего камня. Попробуем рассчитать ходы с длиной 9,10, 11 для камня, стоящего на С4, воспользовавшись формулой:

9 + 4 – 12 = 1

10 + 4 – 12 = 2

11 + 4 – 12 = 3

Так как вторая четверть от С является четвертью А, то к полученным числам необходимо дописать название четверти и получим окончательный ответ:

9 = А1;

10 = А2;

11 = А3.

Ходы с длиной хода от 12 и более это только кушевые ходы – 3:3, 4:4, 5:5, 6:6. Как их подсчитать было рассмотрено в самом начале раздела. Обобщив все вышесказанное, становится ясным, почему именно такая разметка доски в длинных нардах намного упрощает подсчет ходов. Также заметным помощником в подсчете ходов выступает модулярная математика.

Хотелось бы заметить, что данная разметка доски облегчает подсчет именно в длинных нардах, а для коротких нард можно пользоваться любой. Скорее всего раньше широко не применялась разметка доски по четвертям, потому что был сделан перенос «под кальку» разметки доски и з наиболее популярных разновидностей нард – trick trac (от 1 до 12) и backgammon (от1 до 24). Теперь этот стереотипный перенос разметки необходимо изменить на наиболее удобный.

Двухцветная доска.

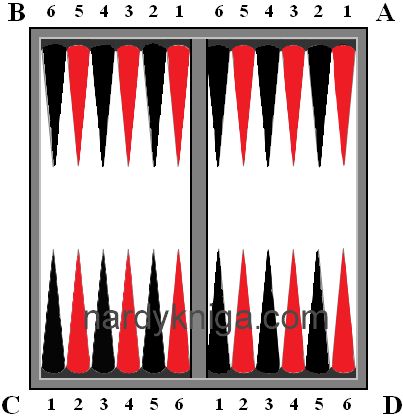В продаже часто можно встретить нарды, где от лунок в середину доски отходит треугольная разметка двух цветов. Например, от нечетных лунок черные треугольники, от четных лунок светлые треугольники (как вариант черного и красного цветов рис. 13.) Такая доска применяется для игры в короткие нарды, но эту разметку можно использовать для облегчения подсчета ходов.

Суть подсчета ходов, используя данную разметку, состоит в следующем: так как цвета чередуются через один, то если камень стоит, допустим, в лунке с черным треугольником и необходимо сделать четный ход, то лунка, в которую надо будет поставить камень, будет такого же цвета (черного), как и лунка, с которой камень стартовал. Если же ход нечетный, то цвет меняется на противоположный.

То же самое можно использовать и в разметке доски от 1 до 6. Здесь также чередуются цифры четные, нечетные. Соответственно при четном ходе лунки совпадают по признаку чет-нечет, при нечетном ходе камень выполняющий ход, должен, поменять порядковый номер лунки с чета на нечет или наоборот.

 

Запас хода. Как быстро его подсчитать.

 

Запас хода одна из главных составляющих в нардах. Игрок, умеющий быстро его подсчитать имеет неоспоримое преимущество над соперником. Отслеживать запас хода в течении всей игры надо не только свой но и противника. Так как нарды игра скоростная, то умение быстро считать запас хода – является свидетельством высшей техники.

Можно обладать математическим дарованием и после каждого хода пересчитывать для всех 30 камней запас хода от 1 до 6.А можно воспользоваться некоторыми рекомендациями позволяющих облегчить эту задачу.

- считать запас хода только для больших свечек;

- считаем запас хода для головы;

- считаем запас хода после кушевого броска;

- считаем запас хода после одинаковых бросков несколько ходов подряд.

Такие подсчеты проводить легко и быстро, так как все вышеперечисленное негативно сказывается на запасе хода, то нет необходимости считать его для всех 30 камней, ведь есть еще и другие задачи в игре.

Достаточно, в некоторой мере владеть информацией о негативе в расстановке камней соперника и постараться его увеличить.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

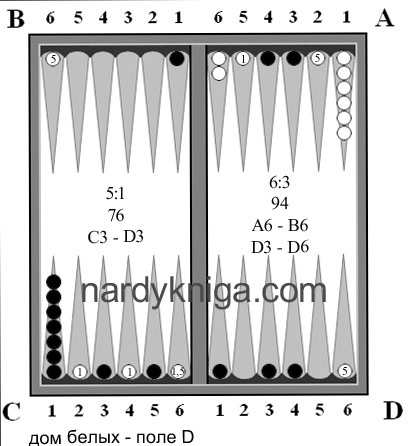
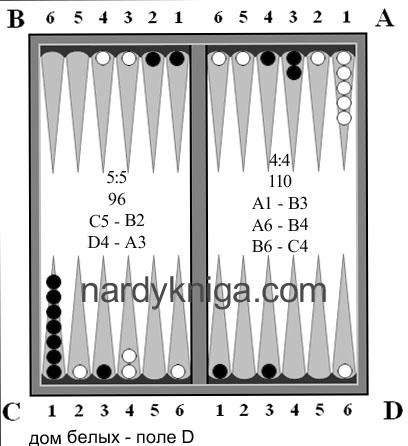
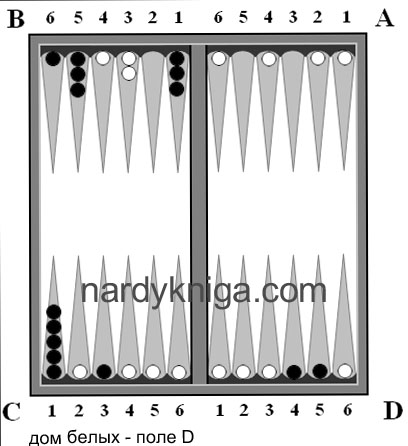
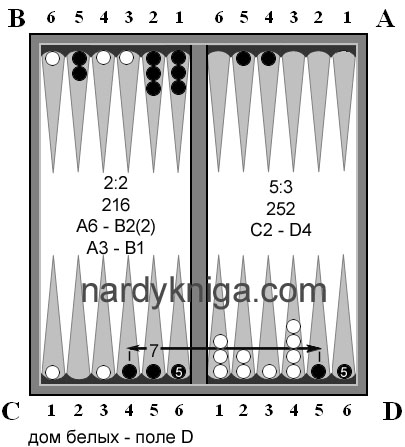
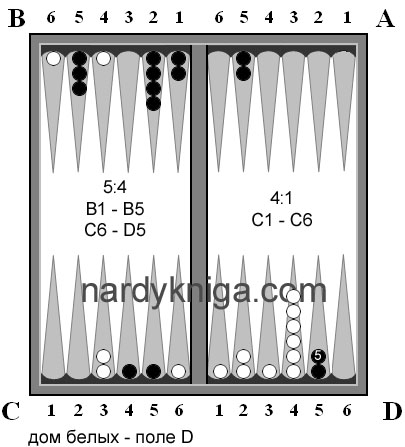
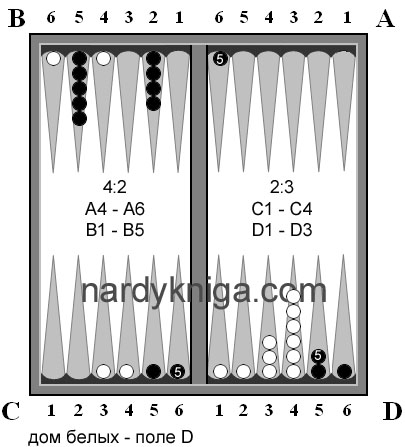
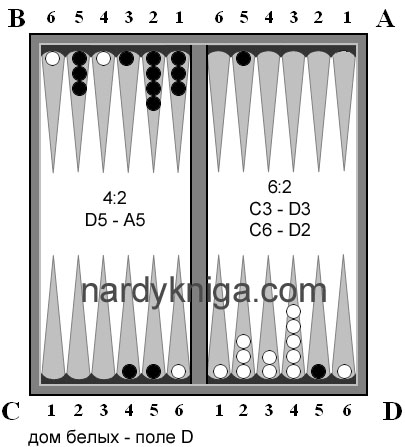
Ситуация, после 9 хода(белые ходят первыми) представлена на рис.1. Белые на 15 очков хотя и опережают черных, но черные совсем неплохо стоят по всему полю и игровую ситуацию на данный момент можно назвать ровной. Как в такой ситуации подсчитать запас хода? Трудно, затратно. Далее белые бросают 6:3 А6 – В6, D3 – D6 (рис.2), в расчете занять В6 и D6 одновременно, что им и удается.

Черные бросают 5:1 и сталкиваются с трудностью выполнения качественного хода и играют просто «по дыркам» С3 – D3. Вот после этого хода черных, белым и надо обратить внимание на запас хода для черных (3-х для головы, 3-х для проблемных ходов). Белые понимают, что им необходимо блокировать ходы черных, содержащих пятерку и единицу. Для этого у белых есть камни на А1, А5, В6, С2, С4, С6, D6. Все эти камни белых на рис.2 отмечены с подписями внутри 1 или 5, показывающие, что они перекрывают потенциально единицу или пятерку. А камень на С6 перекрывает одновременно и пятерку черных С1 и единицу с С5. Поэтому внутри его помешены обе цифры . Далее такой экспресс анализ запаса хода обязывает белых, по возможности, не трогать, без особой нужды, только что перечисленные камни, и посмотреть на развитие игры.

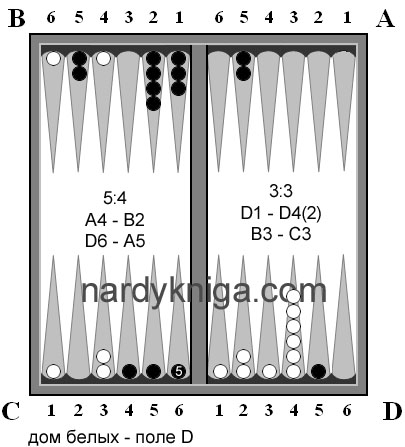
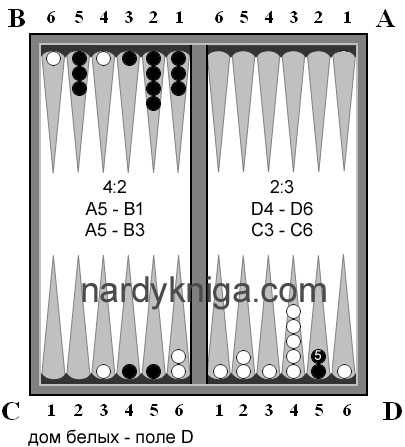
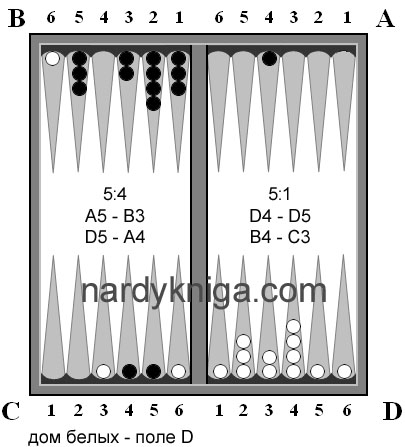
Следующий ход (рис.3). Белые бросают 4:4 и ходят А2 – В4, А6 – В4, В6 – С4. Вызывает вопрос последнее перемещение В6 – С4. Почему не А6 – С2? Белые скорее всего хотят атаковать конец поля С или поле D, для этого перекинули камень на С4. Но самое главное, что они не тронули камни с цифрами внутри, за исключением одного, сделав при этом четыре перемещения.

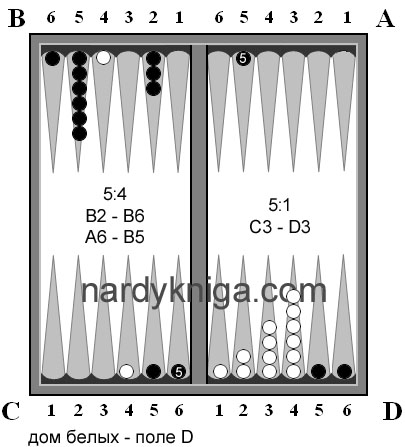
Бросок черных – 5:5. Ход С5 – В2, D4 – А3. Вот снова можно провести экспресс анализ запаса хода после кушевого броска 5:5. Получается, что у черных очень слабо обстоят дела с пятерками. Белые используют это.

 

12. 6:4 А1 – В5 5:3 А4 – В6

13. 5:1 С4 – С5, А1 – А6 6:2 С2 – С3

14. 4:1 А6 – В5 2:3 С1 – С3, D1 – D4

15. 4:2 В4 – С2, С5 – D1 6:5 D3 – А3, С3 – D2

16. 6:1 А1 – А2, В5 – С5 6:5 А3 – В2, D4 – А4

17. 6:1 В5 – С6 5:1 D3 – D4, А3 – В2

18. 4:3 А2 – В3 4:3 В2 – В5, А3 – В1

19. 4:1 А5 – В5 3:3 D2 – D5, В2 – В5(2), А4 – В1

20. 3:3 С2 – D2, С6 – D3, А1 – А4

 

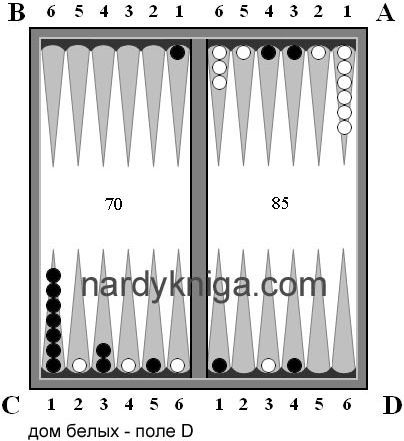
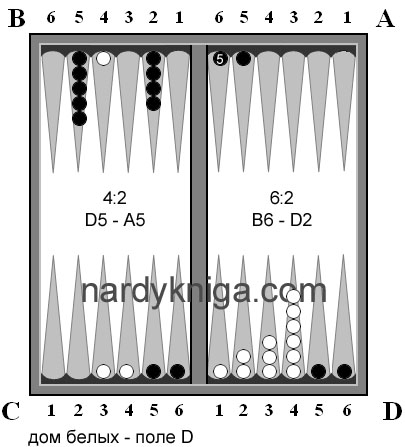
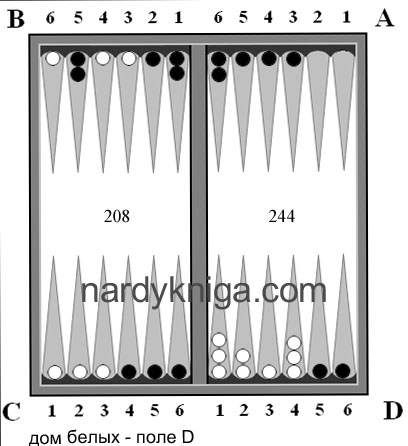Ситуация, представленная на рис. 4, показана после 20 хода белых. Черные согласились на поражение с коксом. На 19-м ходу разница по очкам - +1 в пользу черных. Поэтому, как говорилось ранее, опережение в 15 очков на 9-м ходу мало что значит. Белые оперативно подсчитали дефицит запаса хода у черных и правильно сыграли в дальнейшем.

Рассмотрим еще один пример, связанный с подсчетом запаса хода. В этом примере черные неправильно подсчитали запаса хода после кушевого броска и как результат этой ошибки – проигрыш с марсом.

Для анализа приведем рисунки парами (кроме первого). Слева игровой рисунок, а справа моделирующая ситуация, которая могла бы сложиться, пойди черные правильно.

Ситуация, сложившаяся после 27 хода (черные ходят первыми) представлена на рис.5. По всей видимости, черные проиграют эту партию с оином, так как белые опережают их на 36 очков и расположение белых камней более предпочтительнее в сравнении с расположением черных камней. У черных камень на С4 плохо взаимодействует с камнями на поле D.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

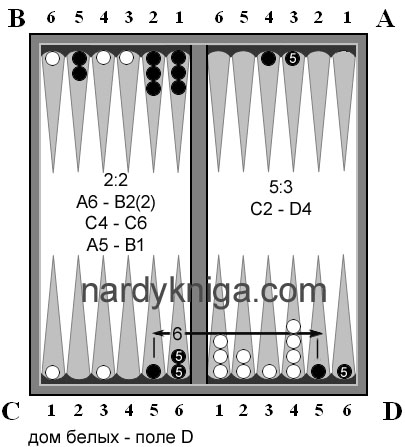
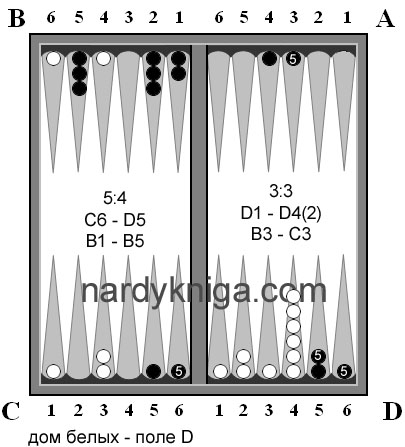
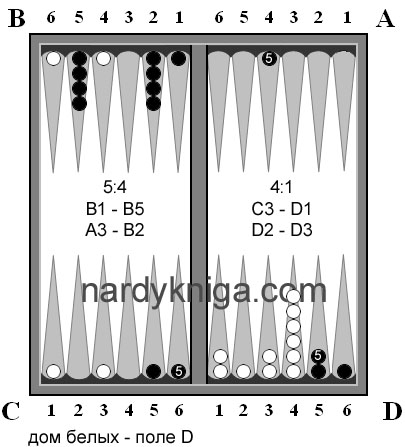
Черные бросают 2:2 (рис. 6) и ходят А6 – В2(2), А3 – В1. Камень на С4 так и остался на расстоянии 7 пунктов от своего камня на поле D. Но к этому добавилось еще одна серьезная проблема – уменьшение запаса хода. Особенно остро стоит вопрос с запасом хода пятерки. Теперь посмотрим на рис.7 – теоретически такое решение более правильное. До поля D не надо «тянуться» через семерку, есть прямая шестерка, а запас хода для пятерки увеличился с двух (рис. 6) до четырех (рис. 7). На обоих рисунках это камни с прописанными пятерками внутри. Далее до пары рисунков 16,17 идет параллельными рисунками развитие игры. Слева реальное, справа – теоретическое возможное. В реальных ходах запас пятерки тает на глазах с каждым ходом. На рис 14 видно, что запаса хода пятеркой для черных нет не считая черного камня на D6, так как убрав его черные подвергают себя угрозе шешара. И вот, к 33 ходу (рис.16) черные «доигрались2 до шешара со стороны белых С6 – D6. Заперев два черных камня на поле D, белые могут выиграть уже не с оином, но с марсом. Посмотрим на виртуальный параллельный рис 17. При такой расстановке черные даже имеют шансы на победу или на поражение с оином. Но однозначно можно сказать, что расположение черных камней на рис.17 намного лучше, чем на рис. 16.

Этот пример реально показывает насколько высокую цену надо платить за неумение быстро подсчитать запас хода после выброса куша.